Ghost Hunter 中微子数据分析排位赛

• 赛事平台
  • 赛事主页 | Ghost Hunter Homepage
  • 得分排行 | Ghost Hunter Leaderboard
  • 代码平台 | Ghost Hunter Gitea
  • 训练数据 | Ghost Hunter Files
  • 状态监控 | DEPSAST Upptime
  • 赛事主页2024 | Ghost Hunter Homepage 2024
• 赛事背景
  • Ghost Hunter 邀请函
  • 赛事介绍与报名
• 赛事信息
  • 比赛题目: JUNO probe
  • 日程安排
  • 评分方式
• 赛事培训
  • 宣讲会
  • probe函数
  • 培训会

Ghost Hunter 邀请函

赛事背景

中微子, 这个被称为“幽灵粒子”的微粒, 自然界的奥秘之一, 质量近似为零, 以接近光速的速度穿越空间, 每一秒数以万亿计的中微子穿过每个人的身体. 然而, 中微子的特殊之处在于它们几乎不与任何物质发生相互作用, 被弱相互作用和引力相互作用所支配, 使得它们难以被探测. 正是由于这一特性, 中微子成为了一种神秘的“幽灵粒子”, 但也正因如此, 中微子具备作为高能“信使”的潜力, 能够将来自宇宙深空的信息传递给我们.

在中微子与物质偶然相互作用的过程中, 带电粒子会产生, 这些粒子会在探测器中释放能量并产生光子. 通过接收这些光信号, 我们可以获取有关中微子的宝贵信息. 江门中微子实验于 2015 年开始建设, 2025 年 8 月 26 日正式运行取数. 这座实验室位于地下 700 米深处, 拥有一个容纳 2 万吨液体闪烁体的探测器, 具有前所未有的 3% 能量分辨率.

借助先进的设备和技术, 中微子的探测变得可能. 在江门中微子实验中, 数以万计的光电倍增管 (Photomultiplier, 简称PMT) 布满探测器外围, 用于接收光信号. 当大量中微子穿越探测器时, 偶尔会在探测器内发生反应, 产生微弱的闪烁光, 这些光信号会被光电倍增管 (PMT) 捕捉到. 通过分析 PMT 的信号, 我们能够获得关于中微子的重要信息.

赛事介绍

本次比赛以中微子探测为背景, 以仿真得到的 JUNO 中心探测器的大量PMT数据为研究对象 Ghost Hunter 们将有机会通过各种数据分析手段, 包括但不限于统计推断、机器学习、物理建模等, 以提升对中微子的能量测量分辨率为目标.

此次比赛面向新手和专家等各种类型的选手, 我们将为您提供详尽的培训和指导, 以确保您能够建立实验物理大数据方法的概念, 并发挥您的潜力. 在比赛中, 您将结识到来自各个院系的同行, 分享知识、经验和创意, 一同挑战学科前沿问题.

Ghost Hunter 中微子数据分析排位赛将为您提供一个展示实力、贡献力量、积累知识与技能的绝佳机会. 我们期待着您的加入, 一同探索中微子的奥秘, 解锁幽灵粒子的秘密!

介绍

赛制介绍

• 赛制: 继承 2021 年至 2024 年的排位赛规则.
• 特色: 本届赛事继承 2024 年的模式, 鼓励各个参赛队伍之间以及新老选手之间进行交流学习. 赛事委员会为选手提供赛事技术交流论坛, 便于参赛选手与前几届入围答辩的前辈进行学术交流; 同时会邀请老选手为新选手进行赛事专题培训, 最终一同参与 Ghost Hunter workshop 交流想法. 但决赛期间不会提供老选手的完整代码.
• 规则: 本比赛为排位赛形式, 每个参赛队伍通过任意的编程语言和数据处理方法, 对组织方提供的仿真数据作为数据集进行分析, 得到数据中实验的能量分辨率作为输出, 在赛事平台上提交最终分析结果. 组织方将通过评判选手提交的结果与标准数据之间的差异, 给出评分排名. 结果可以多次提交, 平台将实时更新各参赛队排名.

赛事支持

1. 赛事基础培训讲座
2. 赛事往届参赛队员讲座
3. 训练数据集、IO代码和测试网站
4. 计算资源支持
5. workshop 论坛选手自由交流讨论

Ghost Hunter Workshop

本届 Ghost hunter 会举办多场 Ghost hunter workshop 研讨会, 来讨论并寻找赛事数据集的最优解, 邀请赛事新老选手一起参加, 形式多样. 参与研讨会的一部分同学需要对自己的成果进行简要汇报, 并基于汇报展开自由讨论, 活动期间参与者可以借助讨论后的灵感在赛事网站进行打榜, 活动末期我们将为参加研讨会并做出突出贡献的同学颁发一系列奖励.

研讨会形式:

1. 人数: 5-15人左右/次
2. 形式: 茶话会等形式, 依据形式提供餐饮
3. 特色奖项: 我们将为在研讨会中做出突出贡献的选手送上我们赛事委员会准备的一系列特色奖项, 具体奖项内容后期会由赛事组参考本期研讨会开展情况决定.

排位赛奖金 (税前)

• 一等奖: 一名, 5000元
• 二等奖: 两名, 2000元
• 三等奖: 三名, 1000元
• 风采奖: 两名, 500元

另外, 我们会为进入决赛的同学准备奖品和奖状.

参赛要求

• 参赛形式: 组队参赛, 每支队伍不超过3人.
• 参赛对象: 不限年级, 不限院系, 不限基础. 鼓励跨院系、跨年级组队. 欢迎兄弟院校同学与社会各界人士参赛.

报名

赛事报名问卷: 清华问卷系统.

如果赛事报名问卷失效或无法加入微信群, 请通过邮件联系清华大学工物科协: depsast@126.com

2025 Ghost Hunter 的赛题: JUNO probe

赛题简介

probe 函数用来描述探测器对顶点的响应, 我们通常将含时的 probe 函数记为 $R(r,\theta,t)$, 该函数表示在相对于 PMT 坐标 $(r, \theta)$ 下随时间 $t$ 变化的 PMT 上接收到的期望 PE 数. 将时间维度积分后, 得到不含时间的 probe 函数 $\lambda(r, \theta)$. 即: 这两个函数之间的关系是: $\lambda(r, \theta) = \int_{0}^{T} R(r, \theta, t) \mathrm{d}t$, 这里 $T$ 是一个足够大的时间窗口, 我们取为 1000ns.

我们已经有了足够好的模拟数据作为训练集, 你需要用这些训练集, 得到一个 probe 函数.

数据集介绍

注: 所有数据集文件均无需手动下载, 使用 Makefile 运行训练或评分时会自动下载.

训练集

训练集文件名如 16001.h5 , 下载后位于 data/ 文件夹下. 每个 h5 文件包含 ParticleTruth 以及 PETruth 两个 dataset, 其格式为:

ParticleTruth

包含 10000 个顶点.

注: Ek 与 Evis 数据在该比赛中可以无需被用到.

PETruth

注: 两个文件中的 PETruth 是对应的; LightTime 数据在该比赛中可以无需被用到.

几何文件

几何文件名为 geo.h5 , 其格式为:

Geometry

测试集

测试集文件名为 concat.h5 , 包含 Concat 以及 Vertices 两个 dataset, 其格式为:

Concat

所有探测到的事件的数据.

Vertices

所有相对于 PMT 的顶点数据.

注: 你可以不用关心 concat.h5 文件, 它的处理已经写好, 且原则上你不能更改. (当然, 你可以使用 concat.h5 来训练, 不过由于我们最终使用隐藏测例进行测试, 所以使用 concat.h5 训练与使用提供的训练集训练并没有实质区别.)

任务说明

任务是修改 probe.py中的 get_mu() 与 get_lc() 函数, 构造出含时与不含时的 probe 函数, 尽量使分数更高. 当前的 probe.py 是依赖于 histogram.py 生成的直方图 histogram.h5 来构造 probe 函数, 如果你采取不同的方案, 也可以删除 histogram.py .

请不要更改 coefficient.py 与 grade.py , 如果发现更改则被视为作弊, 成绩无效. 其它文件均可修改, 也可以添加额外的文件, 但请确保 Makefile 中的 make score 可以正常运行; 如果你发现你引用的包在我们的环境中没有提供, 你也可以与组委会联系, 征得同意后可以修改 ci 以下载包.

我们将提供一个测试集供大家在本地评分作为参考. 但是, 为了防止大家对着测试集过拟合, 本地评测分数及CI排行仅供参考, 最终的排名将由隐藏测例来决定!

附: 评分说明

给定顶点和 PMT 的相对坐标 $(r,\theta)$, 我们可以得到一个 PE 时间序列 $\vec{z} = (t_1,t_2,...t_k)$, 这里 $k$ 是序列长度. 这也是一个非齐次泊松过程, 其似然函数为:

$$P(\vec{z} | r, \theta) = \mathrm{e}^{- \lambda(r, \theta) \mathrm{d}t} \prod_{j=1}^{k} R(r, \theta, t_j)$$

如果我们有 $N$ 次采样, 那么似然函数就是:

$$\mathcal{L} = \prod_{i=1}^{N} P(\vec{z_i} | r_i, \theta_i) = \prod_{i=1}^{N} \mathrm{e}^{- \lambda(r_i, \theta_i) \mathrm{d}t} \prod_{j=1}^{k_i} R(r_i, \theta_i, t_{ij})$$

取对数得到:

$$\log \mathcal{L} = \sum_{i=1}^{N} \left[- \lambda(r_i, \theta_i) + \sum_{j=1}^{k_i} \log R(r_i, \theta_i, t_{ij})\right]$$

评分时, 会将你的 probe 函数 $R(r,\theta,t)$ 与 $\lambda(r, \theta)$ 输入到 $\log \mathcal{L}$ 中, 得到的值越大越好.

为了便于评分, 首先把似然函数的对数值除以评分集顶点数进行归一化 ( 这里的顶点数是在原来的空间中的顶点数, 而不是相对于 PMT 的顶点数, 后者是前者的 PMT_NUM = 17612 倍 ), 然后使用如下函数把分数映射到 $0 \sim 100$ :

$$\text{score}(x) = \begin{cases} 10 \ \exp(x + 17000) \ , & x < -17000 \ (x + 17000) / 100 + 10 \ , & -17000 \le x < -9000 \ (x + 9000) / 500 \times 9 + 90 \ , & -9000 \le x < -8500 \ 100 - \exp[- (x + 8500)] \ , & x \ge -8500 \end{cases}$$

代码

代码文件可以在以下渠道获得:

• GitHub Repository
• Gitea Repository

赛程安排

注: "*" 表示 2025-2026 学年春季学期.

初赛和决赛评分方式

初赛评分方式

初赛根据提交的函数在已公开的测试集上的表现进行评分. 评分标准为模型在测试集上的对数似然函数, 归一化后映射到 $0 \sim 100$, 得分越高则模型越好.

• 初赛截止时间: (清华校历)第十六周周日(2026.1.4) 23:59
• 初赛通过标准 (满足一条即可):
  1. 如果您使用了我们提供的示例代码, 保持基本方法不变并在此基础上展开优化, 当分数超过 60 分时可以入围决赛;
  2. 如果您使用了不同于示例代码的方法, 譬如机器学习、函数拟合、物理分析等, 当分数超过 10 分时可以入围决赛. 如果是这种, 您可以在仓库中新建 report.md 文件并简要说明, 以便我们初赛结算时快速识别.

决赛评分方式

决赛根据提交的代码在未公开的测试集上的表现进行评分, 代码评分标准与初赛相同.

在代码评分的基础上, 决赛还需要提交一份报告. 报告的内容不限于代码实现的描述、代码思路、使用的算法、代码结构等; 报告能够描述清楚即可, 抓住关键点, 不需要面面俱到. 考虑到可能有往届的参赛选手, 如果我们对比报告发现代码变化不大, 您的报告得分将会偏低.

在(清华校历)春季学期第二周周末(2026.3.7)我们预计会举行分享会, 参赛选手可以分享经验与体会等. 参与分享的队伍, 报告会得到一定程度的加分, 但不会超出其所占分数的上限.

• 决赛分数构成:

• 决赛截止时间: (清华校历)春季学期第一周周日(2026.3.1) 23:59

备注信息

1. 初赛与决赛的截止时间均为代码提交的截止时间, ci 运行的评测时间可以超出. 对于初赛, 我们会以截止时间前的提交获得的最高分作为初赛分数; 对于决赛, 我们会以最后一次主分支上的提交在隐藏测试集上的评分作为决赛代码得分, 如果您的代码因为决赛数据集规模变大而无法正常运行, 届时我们可能会采用更换评测服务器等方式在尽量不修改代码的情况下完成评分, 不过您的出分时间可能会延后.
2. 在决赛期间您可以更换您所使用的方法, 不必与初赛相同, 我们鼓励选手们尝试不同的思路, 并且提供了充足的时间安排.
3. 请尽量保持 git 仓库的整洁, 不要将比赛数据集内的文件添加到远程 git 仓库中 (它们已经被 .gitignore 所忽略, 默认是不会被上传的), 如果被发现 git 仓库中上传了比赛数据集文件, 可能会被警告甚至罚分; 你的模型参数文件可以上传, 不会遭到罚分.

赛事宣讲会: 物理背景 & 赛题介绍

前言

在自然界中存在这样一种粒子, 几乎不与任何物质发生相互作用, 它很难被探测, 成为人类眼中的“幽灵粒子”, 它就是中微子. 但总有人热衷于探索自然那不为人知的隐秘, 由清华大学工物系、物理系和计算机系联合举办的“2025 Ghost Hunter 中微子数据分析排位赛”应运而生.

这场“狩猎的盛会”发生在“江门中微子实验中心 (JUNO) ”, 在这片猎场里, 参与者们将获得“猎手”的新身份, 学习“狩猎”的技巧、展现“狩猎”的艺术.

无论您是初学者还是科研领域的专家, 我们诚挚邀请您加入这次场神秘的“狩猎”, 用锐利的眼光和灵活的头脑去巡猎宇宙的奥秘、追寻科学的失落之物、揭开“中微子之谜”的真相. 这片“猎场”等待着您崭露锋芒.

基本信息

• 主讲人: 温欣洋、钱昊远、何宇峰
• 时间: 2025年11月1日 14:00-17:00
• 活动形式: 线下+线上会议
  • 地点: 三教1102
  • 线上会议: 腾讯会议: 112-198-071
• 会议议程:
  1. 14:00-14:30 温欣洋: 介绍 Ghost Hunter 物理背景
  • 物理背景: 中微子, JUNO 中发生的物理过程, Ghost Hunter 的赛事目的与目标;
  • 往届赛题速览.
  2. 14:30-15:30 钱昊远: 讲解 Ghost Hunter 比赛赛题
  • probe 函数的基本含义;
  • 数据集;
  • 评分方式与评分代码.
  3. 15:30-15:40 何宇峰: ssh 配置
  4. 15:40-17:00 答疑与自由交流

材料

• 回放: 清华云盘

probe 函数介绍

理解 probe 函数的含义对该比赛极为重要, 阅读此文档, 能够帮你在宣讲会的基础上更好地理解 probe 函数.

JUNO 探测器中发生的物理过程

JUNO 探测器

在 JUNO 探测器中, 最里面是一个装满了液体闪烁体 (液闪, liquid scintillator, LS) 的大球, 液闪球的半径为 $17.7 ,\text{m}$, 粒子在其中会发光.

外面是一层水球包裹, 水球外面有 17612 个光电倍增管 (Photomultiplier, PMT), 这些 PMT 到球心的距离均为 $19.5 ,\text{m}$ , 其可以看作半径为 $50.8 ,\text{cm}$ 的球体, 且只有朝向探测器中心的那半个球面可以接收光. (这段信息在比赛中并不重要, 除非你要考虑使用物理建模分析的方法.)

在几何文件 geo.h5 的 Geometry 这个 dataset 中, 给出了所有 PMT 的编号与位置信息: 编号为 ChannelID , 从 0 开始; 由于所有 PMT 位于一个球面上, 所以对于位置信息只给出球坐标下的 theta, phi , 注意单位为角度.

顶点

液闪是一种特殊的有机物, 在(正或负)电子的激发下会发生能级跃迁, 各向同性地发出光子, 被 PMT 探测到, 这些发光的点被称作顶点. 顶点的坐标数据对应于训练集中 ParticleTruth 这个 dataset 的 x, y, z ; 而测试集中两个 dataset 的 r, theta , 则是顶点相对于 PMT 的半径归一化球坐标.

通常来说，$\text{MeV}$ 量级的电子可以近似看作一个顶点, 它会迅速在某个位置耗尽所有动能并发出光子, 这是一个非齐次泊松过程, 该过程的典型的时间尺度大概为 $10 ,\text{ns}$ , 其对应训练集中 PETruth 这个 dataset 的 LightTime ; 对于相同能量量级的正电子, 其会先和电子一样消耗能量并发出光子, 然后再发生正负电子湮灭, 产生两个方向相反的、能量为 $511 ,\text{keV}$ 的 $\gamma$ 光子, 由于 $\gamma$ 光子能量较高, 其可能与许多电子发生康普顿散射, 又可以看作一群顶点.

对于中微子的探测, 其发生的典型反应为反 $\beta$ 衰变: $$\widetilde{\nu}_e + p \to e^+ +n$$ 所以, 可以近似的认为中微子发生反应的位置, 亦即正电子产生的位置, 即为顶点.

顶点的动能不会完全转化为发光光子的总能量（也称为可见能量）, 这两个能量分别对应于训练集中 ParticleTruth 这个 dataset 的 Ek 和 Evis , 前者会略大于后者 (你可以在本次比赛中不考虑这两个能量).

PE

顶点发出的光子会在液闪中运动, 到达液闪与水的界面时, 由于液闪的折射率(可取为 $1.48$ )大于水的折射率(可取为 $1.33$ ), 可能会发生折射或(全)反射; 如果折射进入水中, 则其有可能会运动到水与 PMT (表面为玻璃)的界面, 可能会发生折射与反射; 如果进入 PMT , 则会产生光电子(photoelectron, PE), 这就是一个PE.

当然, 在该比赛中, 你可以无需在意上述复杂的光学过程, 而是把重点放在理解顶点与PE的关系上: 一个顶点会产生许多闪烁光子, 被 PMT 探测到的光子会转化为光电子 PE . 从顶点产生到闪烁光子被探测到的时间 (这包括发射光子的时间与光子运动的时间) 对应于训练集中 PETruth 这个 dataset 的 PETime , 以及测试集中 Concat 这个 dataset 的 t ; 在训练集 PETruth 这个 dataset 中, 还包含有闪烁光子命中的 PMT 编号 ChannelID , 可以与几何文件中的 ChannelID 相对应, 还有闪烁光子所来源的顶点编号 EventID , 从 0 开始, 可以与训练集 ParticleTruth 这个 dataset 中的 EventID 相对应.

probe 函数的含义

probe 函数变量的含义 - 顶点相对于 PMT 的半径归一化球坐标

probe 函数 $R(r, \theta, t)$ 或 $\lambda(r, \theta)$ 中的空间坐标 $(r, \theta)$ 是顶点相对于 PMT 的半径归一化球坐标.

其中的"半径归一化"不难理解, 就是把液闪球的半径视为 $1$ , 这样 $r$ 就被限制在了 $0 \sim 1$ 之间, 便于分析, 测试集中的 r 便是如此.

而"相对坐标"要这样理解: 我们在分析时, 把 1 个顶点相对于 17612 个 PMT 的响应, 转化为了 17612 个顶点相对于 1 个 PMT 的响应. 先考虑 1 个顶点对 1 个 PMT 的响应, 我们要以球心为旋转点旋转坐标系, 把 PMT 旋转到最上方的位置, 即球坐标 $r = 1, \theta = 0$ 的位置(或者说直角坐标 $(0, 0, 1)$ ), 顶点的坐标也会跟着旋转, 而对于不同的 PMT , 最终顶点被旋转到的位置是不同的, 这样就把 1 个顶点相对于 17612 个 PMT 的响应转化为了 17612 个顶点相对于 1 个位于最上方的 PMT 的响应, 同时也把一个三维的问题转化为了一个对称的二维问题.

就变量值而言, $r \in [0, 1]$ 为顶点距离球心的位置, $\theta \in [0, \pi]$ 为顶点与 PMT 相对球心的夹角, 如图所示.

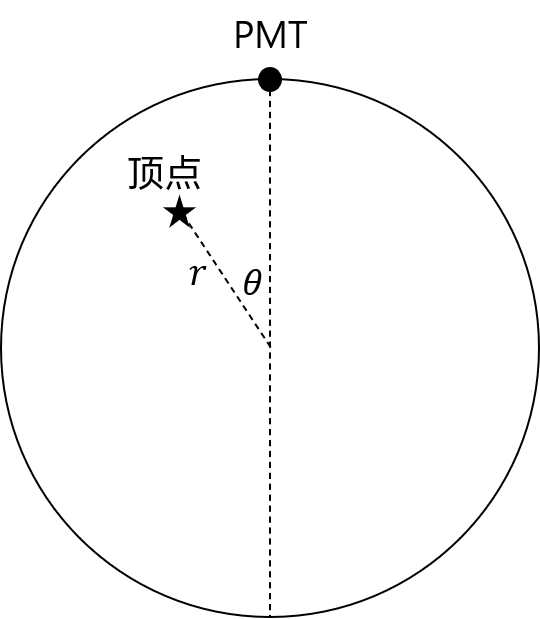
probe 函数值的含义

不含时的 probe 函数 $\lambda(r, \theta)$ 的值, 即为在相对位置 $(r, \theta)$ 的一个顶点, 被最上方的 PMT 探测到的光子数的期望. (根据前面对物理过程的介绍, 其实你可以发现这个函数的值还依赖于顶点的动能, 因为其与顶点放出的光子总数是呈正相关的, 但我们的数据集中顶点的动能是全同的, 所以在该比赛中你无需考虑.)

含时的 probe 函数 $R(r, \theta, t)$ , 即为在相对位置 $(r, \theta)$ 的一个顶点, 在其产生后的时刻 $t$ , 单位时间内被最上方的 PMT 探测到的光子数的期望.

不难发现，含时与不含时的 probe 函数满足: $$\lambda(r, \theta) = \int_{0}^{+\infty} R(r, \theta, t) \mathrm{d}t$$ 再具体实现中, 积分上限通常被取为一个较大的时间, 如 $T = 1000 ,\text{ns}$ .

不含时的 probe 函数可以被绘制为一个圆盘图像, 如下图所示:

probe 函数的构造方法

示例代码提供了一种直方图构造方法.

这里在培训会后会更新一些其它方法的简要说明.

赛事培训会: 基础技能 & 代码讲解

前言

在上次的培训中, 各位猎手认识到了我们的猎物. 面对这么神秘莫测的猎物, 各位猎手必须要装备最好的猎枪和捕兽夹, 本次培训会将聚焦大家手中的工具, 助力大家捕捉那最神秘的幽灵.

在这次的培训中, 每位猎手都将学会使用名为 python 的猎枪, 并为其装上 numpy 与 h5py 的子弹. 与此同时, 你将在 windows 的大地上建起属于你的 Linux 的仓库 (即wsl) , 并使用 git 不断调试你的工具, 为了向幽灵发起最后的奇袭!

哪怕你是第一次成为猎手, 从未尝试过猎人的仓库和猎枪, 也不必畏惧, 要相信你那注定要抓到幽灵的双手. 科协的成员会从最为基础的操作开始, 十分详细地介绍你手中的工具, 即使真的是手无缚鸡之力的书生, 在走出本次培训的会场后, 也会成为冷酷无情的专业猎手.

基本信息

• 主讲人: 刘乐融、张贺、张珺铫、钱昊远
• 时间: 2025年11月16日 14:00-17:00
• 活动形式: 线下+线上会议
  • 地点: 五教5201
  • 线上会议: 腾讯会议: 152-628-127
• 会议议程:
  1. 14:00-14:20 刘乐融: git 基础培训
  • git 的核心概念;
  • git 的基础操作与进阶操作.
  2. 14:20-14:30 张贺: wsl 基础培训
  • Linux 介绍与安装;
  • shell 的基本命令.
  3. 14:30-15:20 张贺: python 基础培训
  • python 基本语法与数据结构;
  • python 调试方法;
  • numpy 的基本用法.
  4. 15:20-15:35 张珺铫: 代码提交与 ci 介绍
  • 使用 git 提交代码至 gitea ;
  • ci 的基本含义以及修改策略.
  5. 15:35-15:50 钱昊远: 示例代码介绍
  • 示例代码的基本思想与代码通览;
  • Makefile 的使用.
  6. 15:50-17:00 答疑与自由交流

预习材料

• windows 下的 wsl2 安装
  1. wsl2 安装教程
  2. wsl2 安装视频
• 如果你是高贵的 macOS 用户
  1. macOS 环境配置
  2. 在 macOS 上使用 UTM 安装 debian
• Linux 基础学习
  1. Linux 基础教程
• git 学习
  1. git CheatSheet
• python 学习
  1. 速通 python
  2. 续本达老师的讲义

材料

• 回放: 清华云盘
• git 讲义: PPT